I'm continuing a blog over at Eric Does Astrophysics if anybody who still follows this cares to read it. It will be less coursework-focused than this, obviously, being not attached to a particular class. Also may involve random interjections of day-to-day life, seeing as nothing happens in a vacuum.
So I guess this is formally the end, over a year belated.
Astronomer, Not Astrophysicist
Eric@CfA: The adventures of a Caltech astrophysics major at the Harvard-Smithsonian Center for Astrophysics.
Friday, May 31, 2013
Tuesday, December 20, 2011
Because Of Science
Note: This post does not have so much to do with astronomy as it does with my feelings about astronomy and how my feelings have evolved. It's going to read very much like a personal blog post. If this does not interest you, stop reading here.
Wednesday, December 14, 2011
An Interview With Jan Vrtilek
As people reading this may know, we had an assignment a while back to interview an astronomer. As we all know, astronomers are busy people. I got one interview back, but Dr. Jan Vrtilek at the CfA was kind enough to fill out an interview when he had time. I first met Dr. Vrtilek several years back as the father of a high school friend. He has since transformed from "my friend's dad" to being a colleague and I had the pleasure of talking with him several times during my SURF at the CfA this past summer. His support and advice were valuable resources.
What is the difference between an astronomer and an astrophysicist at this point in time? Which, if you have a preference, are you?
What are your primary areas of research as an astronomer/astrophysicist? How did you get interested in them?
How did you get into astronomy/astrophysics? What did you study as an undergrad? Where did you go to graduate school and why?
How has your career played out? Is it what you expected? What is the typical career arc of an astronomer/astrophysicist?
How have your goals evolved over the course of your career, if they have at all?
If you hadn't gone into academia, what would you be doing with your education in astronomy/astrophysics?
What is the best part of being an astronomer/astrophysicist? The worst?
What can aspiring astronomers/astrophysicists do to make things easier for themselves? i.e., what do you wish you'd known as an undergrad?
What has been the most difficult stage of your career so far? What have been some notable inspirations along the way?
Any final thoughts for the undergraduate astronomy student?
What is the difference between an astronomer and an astrophysicist at this point in time? Which, if you have a preference, are you?
My short answer would be that there's really no difference at this point in history, and that astronomy/astrophysics is really just a branch of physics (which is why a strong background in physics is likely the optimal preparation for an astronomy/astrophysics career). But a fuller accounting may be a bit more complicated: because astronomy/astrophysics is largely not an experimental science in the usual sense (with exceptions for some areas such as laboratory astrophysics) there is an ongoing history of empirical/statistical/classification studies that can run ahead of a well-developed physical understanding; historically, such work has been associated more with the "astronomy" than the "astrophysics" aspect of the science, and some of these historical associations are still reflected in the subject areas of papers that have shown up in, say, the Astronomical Journal rather than the Astrophysical Journal. But these are small effects, and not something that I think is much worth worrying about.
What are your primary areas of research as an astronomer/astrophysicist? How did you get interested in them?
I work principally in the are of galaxy groups and clusters, with emphasis on the mechanisms of AGN feedback on intragroup and intracluster gas. The decision to work in this area was essentially 'opportunistic': when I joined the Chandra project a couple of years before launch, I had just returned to the CfA from a couple of years working at NASA Headquarters in D.C., and there was an opportunity to move from my earlier area (molecular astrophysics) into a new, potentially very exciting area related to what Chandra would do (and indeed, it turned out that Chandra has made quite remarkable contributions in this area, so it turned out very well).
How did you get into astronomy/astrophysics? What did you study as an undergrad? Where did you go to graduate school and why?
I was a physics and math double major as an undergrad at Wisconsin/Madison. As my undergraduate time was drawing to completion, I know that I would need a specialization, and thought about what area would hold long-term appeal for me. Given my liking for the two astronomy courses that I'd taken, my experience with a quite unusual summer program in high school (the Summer Science program, that has been running for a half century, and is now operated as a nonprofit by its alumni: seehttp://summerscience.org), and the general excitement and promise of the field, the choice wasn't difficult. I applied to a half-dozen graduate schools, and five accepted me. These were days when travel was expensive (at least for me) and there was no internet; I chose Harvard based on rather general considerations and with far less information than a modern student would consider acceptable.
How has your career played out? Is it what you expected? What is the typical career arc of an astronomer/astrophysicist?
In a general sense, it's about what I expected. I never had a single conception of what my future must be ("university professor or bust"), but wanted to be active in forefront work that I found exciting, and my career has done that quite well. Although I did my thesis in active galaxies, the most exciting offer had me going to postdocs and then staff positions at Columbia, Goddard, and the CfA in molecular astrophysics and infrared astronomy. At that point, and with finances running low, I had an interesting offer from NASA Headquarters to join the Visiting Senior Scientist program (alas, it no longer exists) and become a visiting administrator for NASA's infrared and radio astrophysics programs. I had the great good fortune of landing in a team of terrific mentors and colleagues who are still now my close friends, and was able, among many duties, to work as program scientist for COBE, which I think of as one of NASA's greatest missions. I'm not sure that I'd want to do this work forever, but for two and a half years it was a tough but invaluable experience that taught me much about the management and funding of science, but also brought me into touch with a cross-section of the most interesting people and projects of that time. Just as I was finishing up, the Chandra project, a couple years before launch, was staffing its science center, and I was very pleased to get an offer to return to the CfA, in a new life as X-ray astronomer. This also gave me the chance to select a new research area, and I chose X-ray study of galaxy groups and clusters (as described in 'areas of research' above).
Now all of this is hardly "typical", and I suppose that if it teaches a lesson it's that while planning and goals for your career path are necessary and important, what actually happens depends on the unpredictable fluctuations of opportunity. Flexibility is a virtue.
How have your goals evolved over the course of your career, if they have at all?
My goals have always been to "do something interesting" in the field, and I've never been committed a priori to some particular, narrowly-focused area. As a result of this approach, as well as of the practical consequences of managing a two-career family, I've had several switches of subfield. (The plus to this is a thrilling ride through a broad swath of astronomy; the downside is never having that confident settled feeling, but instead the sense of perpetually racing to catch up in the latest area.)
If you hadn't gone into academia, what would you be doing with your education in astronomy/astrophysics?
Given my long association with NASA projects, I suspect that I would be likely to be working in the aerospace industry.
What is the best part of being an astronomer/astrophysicist? The worst?
I'll identify the two most positive aspects for me:
(1) The intellectual excitement and challenge. I hardly have to expand much on this for you -- you're already in the middle of it. For me it has aspects of using physics I like in really cool situations on the grandest scale, a sense of contribution, however modest, to an enduring and worthwhile enterprise, and the pleasure of great variety.
(2) The company of my colleagues. I have been very fortunate in my colleagues and friends. I try to be surrounded by people who are smarter than I am (I strategy I strongly encourage!), and who are also people of decency, humor, and integrity with whom I work on a basis of enduring trust and friendship. This matters immeasurably to the quality of life.
As to the worst, there are the inevitable exhaustion, frustration, and uncertainty. But you are not likely to escape occasional encounters with these in any challenging profession, and there is no line of work that I can think of these days that will offer you a sure path to peace and security!
What can aspiring astronomers/astrophysicists do to make things easier for themselves? i.e., what do you wish you'd known as an undergrad?
I can't offer much more here than the obvious: get a really solid physics and math background. Work with a strong sense of strategy. Find good advisors and listen to them. Find talented, reliable, congenial collaborators.
There is maybe one point at which particular care is warranted. When you're going for your PhD, your choice of advisor and research group is critical. This is a spot where problems can arise that cost you much time and frustration. You'll want to assess very carefully the project (for how workable it is and how it will place you for your future plans), the advisor (for success with earlier students), and the entire team (for the "spirit" and effectiveness of the group).
What has been the most difficult stage of your career so far? What have been some notable inspirations along the way?
I suppose the very high level of uncertainty at various points, especially early on. There was a whole series of moves at 2 or 3 year intervals, which means being in job-search mode about half the time. It came with the uncomfortable realization that there's a fair amount of luck involved; I've gone through searches with only one offer at the end, and that makes the role of chance all too clear. I can't say too much about the importance of a really positive and supportive personal life to sustain you through the difficult spots, and to help you enjoy the smooth stretches!
Any final thoughts for the undergraduate astronomy student?
Not at the moment. You have a good set of questions! If there's anything you'd like me to clarify or expand on, please just let me know.
Sunday, November 20, 2011
Two-Body Orbits: Where's The Centre of Mass?
Second Authors: Nathan, Lauren
Introduction
Consider a problem of a planet orbiting a star. It's easy to see from Newtonian gravitation that they exert a force on one another. But then, how, according to Kepler's Third Law can we say the planet orbits the star alone? The star cannot remain fixed while feeling a force. In order for Newton's Laws to hold, we must say that they both orbit a mutual centre of mass. Using conservation of momentum, we can determine how far each body truly is from this centre of mass.
Methods
In order to balance forces, we notice that the planet and the star must be at opposite ends of their orbits at all times as seen in the following picture (not to scale). It follows from this that they have the same orbital period and the same angular velocity.
We know that linear momentum is equal around the centre of mass, such that:Dividing through, we get the relationship
Rearranging and using the mean semimajor axis, a, we can see that
Conclusion
We have shown here that star does indeed orbit the centre of mass, just as the planet does. However, looking at these equations carefully, we find that except for very massive planets, the semimajor axis of the star's orbit is roughly zero and the semimajor axis of the planet's orbit is roughly equal to the mean semimajor axis. As a result, we find that we can in fact use the assumptions implicit in Kepler's Law.
The Death of a Star
Second Authors: Nathan, Lauren
Introduction
We know how stars are formed to a certain extent and that while they are on the main sequence, they are supported by hydrostatic equilibrium. However, when a star moves off the main sequence and can no longer support itself, what happens? We assume that at this point, the core of the sun has converted all of its mass to energy and is now undergoing gravitational collapse.
Methods
We know that the Sun generates energy throughout its lifetime at a rate of:
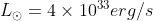
Assuming that the sun uses up the entire mass of its core (10% of a solar mass) as it undergoes fusion, and converts energy with 0.7% efficiency, we can determine the total energy it produces in its lifetime with
\left ( 9 \times 10^{20} cm^{2}/s^{2} \right )=1.26 \times 10^{51} ergs)
Dividing this number by the rate of energy production, we can determine the time it takes for the Sun to use all of its mass available for fusion. This time is
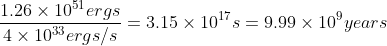
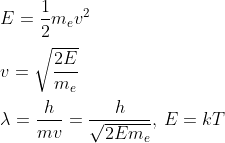
It is easy to tell that we have one molecule per cubic lambda. So we have:
^{3})
The actual value is 8 times this, for reasons I can't remember, but Nathan tells me Professor Johnson said the factor of 8 was okay to include in our calculations. So multiplying this by the mass of a hydrogen atom and using T = the temperature of the sun's core, we get density
^{\frac{3}{2}}}{h^{3}}m_{H}\approx 360 \; g/cm^{3})
Which is more than twice the current maximum density of the sun's core.
Conclusions
We find that by converting 0.7% of the mass of the sun's core into energy, the sun's lifetime is roughly 10 billion years, which agrees with what scientists have predicted. The density of the core after collapse will also be far greater than the current density of the sun's core, which is reasonable or it would not be able to support the sun post-collapse.
Introduction
We know how stars are formed to a certain extent and that while they are on the main sequence, they are supported by hydrostatic equilibrium. However, when a star moves off the main sequence and can no longer support itself, what happens? We assume that at this point, the core of the sun has converted all of its mass to energy and is now undergoing gravitational collapse.
Methods
We know that the Sun generates energy throughout its lifetime at a rate of:
Now we know the core will collapse, but it won't collapse indefinitely. We find that the core collapses to the point that the interparticle spacing is on the order of the De Broglie wavelength. Since it is easy to see that electrons have greater momentum compared to protons of equal energy, electrons are the first to reach this critical density. We can calculate this using the equations:
It is easy to tell that we have one molecule per cubic lambda. So we have:
The actual value is 8 times this, for reasons I can't remember, but Nathan tells me Professor Johnson said the factor of 8 was okay to include in our calculations. So multiplying this by the mass of a hydrogen atom and using T = the temperature of the sun's core, we get density
Which is more than twice the current maximum density of the sun's core.
Conclusions
We find that by converting 0.7% of the mass of the sun's core into energy, the sun's lifetime is roughly 10 billion years, which agrees with what scientists have predicted. The density of the core after collapse will also be far greater than the current density of the sun's core, which is reasonable or it would not be able to support the sun post-collapse.
Friday, November 18, 2011
An Interview With an Astrophysicist: The Postdoc
As some readers may know, this past summer I had the privilege of being able to work for Dr. Andy Goulding at the Smithsonian Astrophysical Observatory. Dr. Goulding is a first year Smithsonian Research Fellow in the High Energy Astrophysics division. He did his PhD work in AGN activity at the University of Durham, UK in the fall of 2010 before moving to Boston as a postdoc. Working with him was a wonderful educational experience that I'd happily do over if I had the chance. He gave me a look into the life of a researcher and how much research differs from course work.
We've vaguely kept in touch since September and he generously agreed to answer a few questions on his career for me. Of course, given the title of this blog, the first question was obvious. He took a lot of time in answering these questions, and I definitely learned some new things. For example, I had no idea that there was a difference between a postdoctoral research associate and a fellow.
What is the difference between an astronomer and an astrophysicist at this point in time? Which, if you have a preference, are you?
From a professional point of view, this is really semantics. People have degrees/PhDs in astronomy and/or astrophysics - it depends on institution. However, it is more likely that someone who is an amateur (non-PhD) is considered to be an astronomer. Classically, an astrophysicist attempts to understand and interpret the astronomical observations through application of physics. My PhD is in astrophysics, so in the strictest sense, I am an astrophysicist.
Sunday, November 13, 2011
Star Formation: Timescale and Stability
Introduction
Star formation is governed by the collapse of a cloud of particles into a gravitationally bound sphere which we call a star. The radius of the could at which this occurs is called the Jeans Length, where the gravitational force of the cloud overcomes the thermal energy causing it to expand. Here we examine the time scale of such a collapse and also calculate the Jeans Length.
Methods
In order to determine the time it takes for this collapse to occur in terms of the mass and size of the cloud, we consider a cloud of mass M and a test particle a distance away from it. We assume the cloud has a mass given by
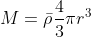 where r is the length of the major axis for an elliptical orbit of eccentricity 1. By assuming such a geometry for the free fall, we can initially approximate the orbit to a straight line with a mass M at one end and our test particle at the other. Since this is a free fall, we can also approximate the time tff to be half the orbital period we get from Kepler's 3rd law (a = 1/2 r)
where r is the length of the major axis for an elliptical orbit of eccentricity 1. By assuming such a geometry for the free fall, we can initially approximate the orbit to a straight line with a mass M at one end and our test particle at the other. Since this is a free fall, we can also approximate the time tff to be half the orbital period we get from Kepler's 3rd law (a = 1/2 r)
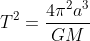 Substituting our mass formula into this equation, we get
Substituting our mass formula into this equation, we get
^{3}}}=\sqrt{\frac{3 \pi}{32G\bar{\rho}}}) The implicit assumptions are that we can even call this half an orbit, as an eccentricity 1 orbit is parabolic and therefore not periodic, and that we can approximate this orbit to a straight line. Now in order to find the Jeans Length, we equate this to the dynamical time, or the time it takes a sound wave to cross this distance. Let's define this as
The implicit assumptions are that we can even call this half an orbit, as an eccentricity 1 orbit is parabolic and therefore not periodic, and that we can approximate this orbit to a straight line. Now in order to find the Jeans Length, we equate this to the dynamical time, or the time it takes a sound wave to cross this distance. Let's define this as
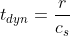 Equating the two, we get the radius at which the cloud will undergo gravitational collapse
Equating the two, we get the radius at which the cloud will undergo gravitational collapse
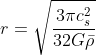 For an isothermal gas of constant density, this length signifies the minimum radius at which it will continue to be a gas and not collapse into a much denser formation. This is the Jeans Length to an order of magnitude. The actual formula for the Jeans Length is
For an isothermal gas of constant density, this length signifies the minimum radius at which it will continue to be a gas and not collapse into a much denser formation. This is the Jeans Length to an order of magnitude. The actual formula for the Jeans Length is
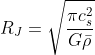
Conclusions
We have hear calculated the free fall time for star formation as well as the radius at which the gravitational force between interstellar dust particles takes over. It is important to note that since the density is radius dependent, the Jeans Length is not constant for all star forming clouds, but varies even with the change of radius due to collapse and we have
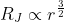 If we consider a cloud that starts out at the Jeans Length for its particular conditions, by the time it reaches half this radius the Jeans Length has decreased by a factor of √8. As a result, the initial Jeans Length may actually govern how far the cloud will collapse for a given mass and radius.
If we consider a cloud that starts out at the Jeans Length for its particular conditions, by the time it reaches half this radius the Jeans Length has decreased by a factor of √8. As a result, the initial Jeans Length may actually govern how far the cloud will collapse for a given mass and radius.
Star formation is governed by the collapse of a cloud of particles into a gravitationally bound sphere which we call a star. The radius of the could at which this occurs is called the Jeans Length, where the gravitational force of the cloud overcomes the thermal energy causing it to expand. Here we examine the time scale of such a collapse and also calculate the Jeans Length.
Methods
In order to determine the time it takes for this collapse to occur in terms of the mass and size of the cloud, we consider a cloud of mass M and a test particle a distance away from it. We assume the cloud has a mass given by
Conclusions
We have hear calculated the free fall time for star formation as well as the radius at which the gravitational force between interstellar dust particles takes over. It is important to note that since the density is radius dependent, the Jeans Length is not constant for all star forming clouds, but varies even with the change of radius due to collapse and we have
Subscribe to:
Posts (Atom)
